All Sensors Pressure Points are application tips to simplify designing with microelectromechanical (MEMS) pressure sensors and avoiding common pitfalls.
Pressure Point 1: MEMS Pressure Sensors - Pressure Measurement Types
Microelectromechanical system (MEMS) pressure sensors have changed the way that system designers and application engineers measure pressure. The simplicity of use, small size, low cost and ruggedness allow these sensors to address applications in automobiles and industrial process control as well as medical and handheld portable products. For example, a highly accurate altitude measurement in a handheld navigation device such as a smartphone that has three-axis accelerometers, gyroscope and magnetometers adds a tenth degree of freedom. Pressure sensing allows the navigation device to locate the exact floor of a destination.
MEMS pressure sensors typically measure the pressure difference across a silicon diaphragm. As shown in Figure
1, there are three types of measurements:
• Gauge or gage (a) , where the pressure is referenced to the atmosphere
• Absolute (b) where the pressure is measured against a reference vacuum sealed inside the chip assembly
• Differential (c), where the pressure is measured as the difference between two pressures (delta P or ΔP)
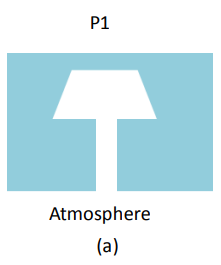
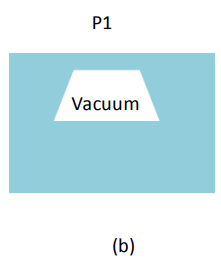
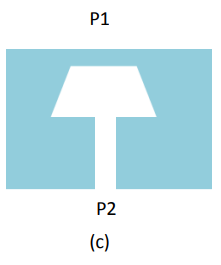
Figure 1. Gage, absolute and differential pressure measurements have different types of pressure on each side of the diaphragm.
In these designs, the diaphragm is etched from silicon using micromachining, a chemical etching process. The measurement technique can involve capacitive or resistive (piezoresistive or pressure sensitive resistors). Piezoresistive designs are shown in Figure 1. Vacuum is a negative gauge pressure or a value below atmospheric pressure. When specifying or discussing the type of pressure measurement, it is essential to identify the type of measurement to convey an accurate description of the measurement technique. Table 1 shows the sensor requirements for several common measurements.
Application requirements for absolute, gauge and differential pressure sensing
| Measurement | Type | Value (nominal) |
|---|---|---|
| Atmospheric pressure | absolute | 760 Torr (101.3 kPa) |
| Altitude | absolute | Look up table/calculate |
| Manifold pressure (vehicle) | absolute | 100 kPa |
| Depth in water | absolute | Calculate |
| In vivo blood Pressure | absolute | 80/120-mm (300 mm Hg, max) |
| Ex vivo blood pressure | gauge | 80/120-mm (300 mm Hg, max) |
| Height of liquid column | gauge | Calculate |
| Intraocular pressure | gauge | 15 mm Hg |
| Tire pressure | gauge | 30 psi |
| Vacuum cleaner | gauge | 760 to 25 Torr (100 to 3 kPa) |
| Liquid or gas flow | differential | Application dependent |
| Respirator | differential | 4 kPa |
| Ventilator | differential | 25 cm H20 |
| Spirometer | differential | 4 kPa |
Table 1. Common pressure measurement versus type of measurement.
Atmospheric Pressure and Altitude
Perhaps the most fundamental pressure measurement is atmospheric pressure. Standard atmospheric pressure at sea level is 29.92 inches of mercury (Hg) (760 mm Hg (Torr) or 14.696 psi). The atmospheric pressure decreases with increasing altitude and increases at altitudes below sea level. Weather patterns with low and high fronts decrease or increase atmospheric pressure. An aneroid barometer provides an absolute pressure measurement.
An altimeter is an absolute pressure gauge (measurement) that shows height above sea level. The air pressure to height above sea level conversion is frequently performed using a look up table. For example, 10,000 feet above sea level is 10.1 psia (69.7 kPa). Pressure altitude (halt) can be calculated using the equation:
halt = (1-(psta/1013.25)^0.190284)x145366.45 Eq. 1
Where:
halt is the height in feet and psta is the pressure in millibars (mb) or hectopascals (hPa)
Height of a Liquid Column
For a standing liquid, the absolute pressure at a depth H in a liquid is defined as:
Pabs = P + (ρ x g x H)
Where: Pabs is the absolute pressure at depth H in kg/m-s 2 (or Pa) P is the external pressure at the top of the liquid, typically atmospheric pressure for open systems ρ is the density of the fluid (for example, pure water is 1 g/cm3 at 4°C and salt water is 1.025 g/cm3 ) g is the acceleration due to gravity (g = 9.81 m/s2 ) (32.174 ft/s2 )) and H is the depth in meters or feet
Depth in Water
The pressure on submerged bodies increases based on the density of the liquid and depth in the liquid according to Eq. 2. Common measurements include depth in fresh or salt water. For fresh water, pressure increases 0.43 psi per foot and in salt water it is 0.44 psi per foot. A scuba diver’s submersible pressure gauge (SPG) or depth gauge makes an absolute pressure reading. A dive computer provides the time required for a safe ascent, since even a depth of 100 feet can produce a pressure of 400 kPa (3.951 atmospheres, or 58.1 psi).
Flow in a Pipe/Tube
Several factors determine the pressure drop that occurs in fluid flow applications including laminar versus turbulent flow, the flow velocity, kinematic viscosity and Reynolds number of the fluid, internal roughness of the inside of the pipe as well as its diameter, length and form factor. Orifice plates, venturi tubes and nozzles simplify the situation. In these cases (refer to Figure 2), the flow is related to ΔP (P1-P2) by the equation:
q = cd π/4 D22 [2(P1 - P2) / ρ(1 - d4) ]1/2
Where:
q is the flow in m3/s
cD is the discharge coefficient, the area ratio = A2 / A1
P1 and P2 are in N/m2
ρ is the fluid density in kg/m3
D2 is the orifice, venturi or nozzle inside diameter (in m)
D1 is the upstream and downstream pipe diameter (in m)
and d = D2 / D1 diameter ratio

Figure 2. Elements of a ΔP flow measurement.
Pressure Parameters
As the examples demonstrate, pressure measurements use a variety of pressure standards to express the reading depending on the application. To convert between different pressure standards:
http://www.wrh.noaa.gov/slc/projects/wxcalc/formulas/pressureConversion.pdf
